human and environment

4-3. データの解析と評価

- ヒトからみた環境 - 　玉利祐三

4-3-4. 相関関係: 相関と相関係数
　二つの事柄、例えばＸとＹがあり、それぞれが変化（変数）するとき、ＸとＹの間に相関があるのか、ないのかを判断することがあります。例えば、中学校のあるクラスで全生徒の体重（Ｘ）と身長（Ｙ）に相関関係がみられるのかどうかとか、他の例では血液中のある成分濃度（Ｘ）が上昇すれば、ある症状の発症率が高くなるのかどうか等のような場合に相当します。これを理解し、評価するにはまず基本的な知識が必要です。

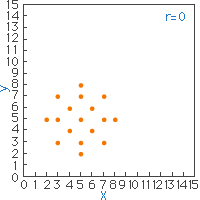図16	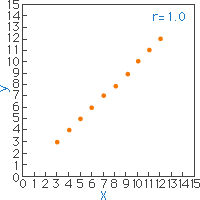図17
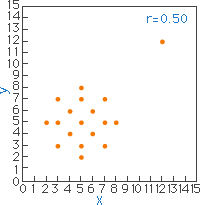図18	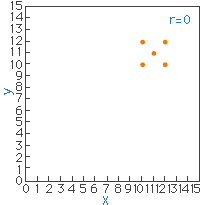図19
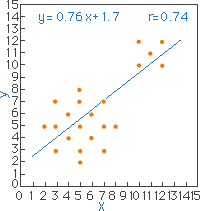図20

　図16は、ＸとＹについていくつかのデータを図示したものですが、散布図が円状であり、ＸとＹとの間には相関が見られず（無相関）、相関係数r=0となります。相関係数とは、相関の程度を数値（-1～＋1）で示すもので、

-1.0	≦ ｒ＜	-0.7	強い負の相関がある
-0.7	≦ ｒ＜	-0.4	かなり負の相関がある
-0.4	≦ ｒ＜	-0.2	やや負の相関がある
-0.2	≦ ｒ＜	0.2	ほとんど相関がない
0.2	＜ｒ ≦	0.4	やや正の相関がある
0.4	＜ｒ ≦	0.7	かなり正の相関がある
0.7	＜ｒ ≦	1.0	強い正の相関がある

とおおよその判断ができます（縣　俊彦、やさしい栄養・生活統計学、南江堂、37頁、1997）。ただし、標本数（試料数）が少ない場合にはこのような判断がされるとは限りません。

　図17は、ＸとＹの間に強い正の相関がみられ、相関係数ｒ=1.0となります。しかし、相関を調べるとき一つの試料（標本）が加わっただけで図18となり、相関係数はｒ=0.5となり、あたかも正の相関があるようにみえるのです。図19では前述と同様に無相関ですが、図20では二つのグループを一つとみなし相関係数を算出すればｒ=0.74となり、見かけ上は強い正の相関があることを示してしまいます。

　図20のように、結論の間違いは図16と図19の別のグループ（母集団）を一つのグループ（母集団）として取り扱い、相関を評価したことが間違いなのです。統計処理する試料（標本）の選定が間違ったために起きたものです。

　任意に、平等に母集団から標本（サンプル）を選ばなければなりませんが、実際に行われる動物実験のデータ等では、これが非常に難しいのです。さらに、母集団から選ぶ標本数（サンプル数）が多ければ結論の信頼性は高くなりますが、現実の動物実験のデータ等では実験上の制約が色々とあるので、実験数（標本数）を増やすことには限界があります。

　このように統計処理では、試料（サンプル）の選び方、試料の数という前提条件が結論に大きな影響を及ぼすことになります。従って、一般的には試料数を考慮して相関係数を算出する必要があります。

相関検定と有意水準
　相関図（散布図）や相関係数は、パソコンで普通の統計ソフトを使用すると、だれでも簡単に作図ができ、また相関係数を算出することもできます。しかし、単なる相関係数の値や相関図から相関の有無を結論づけることは危険です。

　そこで、相関があるのか、ないのかを検定する必要があります。まず、ＸとＹの二つの変量の間に"相関がない"と仮説をたて（そのため対立仮説は、"相関がある"となります）、一定の有意水準の値でこの仮説を検定することになります。勿論、これには相関係数の値、有意水準の設定値、標本数などから算定し、相関があるか、ないかを結論づけます（つまり、検定するわけです）。この検定処理をコンピュターで行う場合、信頼できる専門的なソフトが一般的に使用されます。学術研究分野では、SAS (Statistical Analysis System)、SPSSX（Statistical Package for Social Science X)、Stat View等がよく使用されています。

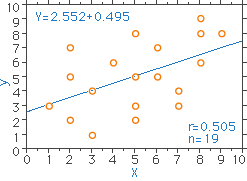
図21 相関がみられる(検定: p<0.05)

図22

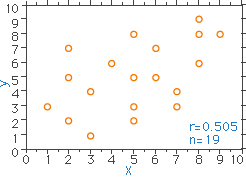
図22 相関がみられない(検定: p<0.01)

図23

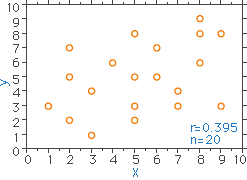
図22 相関がみられない(上図に一点追加)
(検定: p<0.05 及び p<0.01)

　三つの図の例では、標本数（実験データ等）が19で、有意水準を0.05（危険率を5％）としたとき、相関計数r=0.505となり、検定の結果"相関がある"と結論づけられます（上側、図21）。しかし、これと全く同一のデータでありながら、有意水準を0.01（危険率1％）と設定変更すれば、相関係数はr=0.505と同じなのですが、検定の結果は"相関がない"となります（中間、図22）。どちらも正しい結論なのですが、有意水準の設定値が少し異なるだけで、このようなことになるわけです。

　このような19の標本数（試料数）に1サンプルのデータが加わると（標本数は20）、上側の二つの図とほとんど同じように見えますが、相関係数を算出するとr=0.395となり、有意水準を0.05で検定しても、0.01で検定してもどちらの場合も"相関がみられない"　との結論になります（下側、図23）。このように、1点が図に加わるだけで、結論が大きく変わるのも"相関"なのです。

　また、サンプル（標本数）が数百、数千のようにかなりの数があるときには、たとえ相関係数が低くても（例えば、r=0.2...）、検定の結果、相関が認められることもあります。

　以上のように相関関係の評価はかなり難しいことがご理解して頂けたことと思います。詳しくは、統計の専門書をご覧になって下さい。